Broaching Forces
A broaching operation has a large variation in strength during the process and the most important value is the maximum force required. It is with this value that we can determine the equipment that will perform the operation, but understanding how and why the force varies during the machining is an important step to understand it fully.
Calculating the Cutting Forces
During the operation the number of teeth cut simultaneously (n) is “constant” and can be calculated by the expression
n = L / p
where L = length to be broached and p = pitch of the teeth of thinning. It should be noted that if the value is not an integer, always rounds up.
The maximum force in the operation of grinding can be calculated by expression:
Fmax [kg] = a[mm2] * re [kg/mm2] * n
A = area of material removed, re = specific resistance of cutting, and n = number of cutting teeth simultaneously. As the shape of the teeth varies, the value of A also varies and therefore the value of the force as well. In addition there is a change in the number of teeth in cut simultaneously when n is not integer, generating a fluctuation.
Calculation example
Here is an example to simplify understanding. Suppose you need to broaching an eight-slot hole, as shown below, on a piece of steel with a thickness of 32 mm and a specific cutting resistance is 315 kg/mm2.
The broach has 12 mm pitch and step forward thinning of 0.05 mm.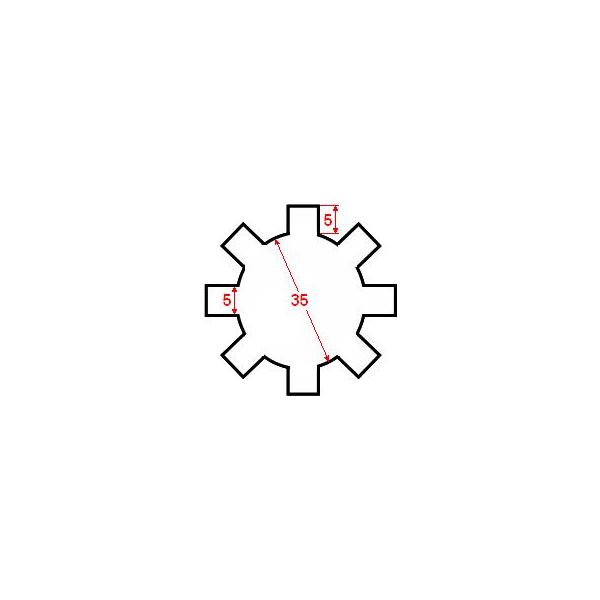
First step: Calculating the number of teeth cut simultaneously (n):
n = L / p
n = 32/12 = 2,667
n = 2,667
n = 3 teeth
Second step: Calculating the area of material to be removed (A)
A = 8 * (5 * 0.05)
A = 2 [mm2]
Third step: Calculation of the maximum force in Broaching (Fmax)
Fmax = 2 * 315 * 3
Fmax = 1890 [kg]
Fourth and last step: Calculation of force at the beginning of grinding
At the beginning of the operation, before joining the scheme, we have only 1 tooth in contact with the piece. In this case the force is F1 = 630 [kg]. Shortly thereafter comes into the second tooth and the force will be F2 = 1260 [kg].


